Contoh Soal Fisika Kelas Xi Semester 1 Gerak Parabola Soal Bahasa

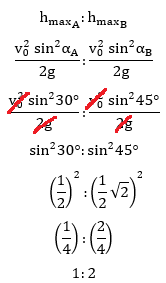
Aug 3, 2018 - GRUB is the of the 's, which provides a user the choice to boot one of multiple. Comfy easy pc software download for windows. Contoh Soal Fisika Kelas Xi Semester 1 Gerak Parabola Soal.

RUMUS-RUMUS FISIKA SMP NO RUMUS SIMBOL SATUAN (SI) INFORMASI PENTING 1 Massa Jenis ρ = ρ = massa jenis m = massa v = volum Kg/m3 Kg m3 1 g/cm3 =1000 Kg/m3 1 Kg/m3 = 0,001 g/cm3 2 Pemuaian panjang zat padat = pertambahan panjang = panjang mula-mula = koefisien muai zat padat ∆T = perubahan suhu = panjang akhir m m /oC atau /K oC m Khusus bagian ini dan tidak harus dalam meter asalkan satuan keduanya sama misal dalam cm 3 Kalor a. Kalor untuk menaikan suhu benda Q = m.c.∆T b. Kalor untuk merubah wujud benda Q = m.L c. Asas Black m1.c1.(T1-Tc) = m2.c2.(Tc-T2) d.

Projectile Motion, General Solution What follows is a general solution for the two dimensional motion of an object thrown in a gravitational field. This is usually termed a projectile motion problem. The thrown object is called the projectile. Its path is called the trajectory.

We will answer all the usual questions that arise in a first year physics class regarding this motion. We will not consider air resistance. Without air resistance, the projectile will follow a parabolic trajectory. We will be throwing the projectile on level ground on planet Earth. It will leave the point of release, arc through the air along a path shaped like a parabola, and then hit ground a certain distance from where it was thrown.

As mentioned above, this is a two dimensional problem. Therefore, we will consider x and y directed displacements, velocities, and accelerations. The projectile will accelerate under the influence of gravity, so its y acceleration will be downward, or negative, and will be equal in size to the acceleration due to gravity on Earth. There will be no acceleration in the x direction since the force of gravity does not act along this axis. On Earth the acceleration due to gravity is 9.8 m/s 2 directed downward. So, for this presentation acceleration in the y direction, or a y, will be -9.8 m/s 2, and acceleration in the x direction, or a x, will be 0.0 m/s 2.

Given the original conditions with which the projectile is thrown we will proceed to find the components of the original velocity and then move on to answer the following questions: • How much time passes till the projectile is at the top of its flight? • How high does the projectile rise? • How much time passes till the projectile strikes the ground? • How far away does the projectile land from its starting point?

Original, or initial, conditions: The original conditions are the size of the velocity and the angle above the horizontal with which the projectile is thrown. General: Original size of velocity: v o Original angle: theta Example: v o = 40.0 m/s theta = 35 degrees Components of original velocity: The usual first step in this investigation is to find the x and y components for the original velocity. General: X component of original velocity: v ox = v ocos(theta) Y component of original velocity: v oy = v osin(theta) Example: In the x direction: v ox = v ocos(theta) v ox = (40.0 m/s)(cos(35 degrees)) v ox = (40.0)(0.8191) v ox = 32.76 v ox = 32.8 m/s In the y direction: v oy = v osin(theta) v oy = (40.0 m/s)(sin(35 degrees)) v oy = (40.0)(0.5735) v oy = 22.94 v oy = 22.9 m/s How much time passes until the projectile is at the top of its trajectory? At the top of the trajectory the y, or upward, velocity of the projectile will be 0.0 m/s. The object is still moving at this moment, but its velocity is purely horizontal. At the top it is not moving up or down, only across.

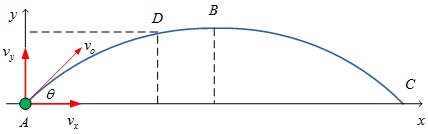
Notice that the object is still in motion at the top of the trajectory; however, its velocity is completely horizontal. It has stopped going up and is about to begin going down. Therefore, its y velocity is 0.0 m/s. We need to find out how much time passes from the time of the throw until the time when the y velocity of the projectile becomes 0.0 m/s. This y velocity at the top of the trajectory can be thought of as the final y velocity for the projectile for the portion of its flight that starts at the throw and ends at the top of the trajectory. We will call this amount of time ‘the half time of flight’, since the projectile will spend one half of its time of flight rising to the top of its trajectory. It will spend the second half of its time of flight moving downward.

General: We can use the following kinematics equation: v f = v o + at Subscript it for y: v fy = v oy + a yt Solve it for t: t = (v fy – v oy) / a y Plug in 0.0 m/s for v fy: t = (0.0 m/s – v oy) / a y If the original y velocity and the y acceleration, i. E., the acceleration due to gravity, are plugged into the above equation, it will solve for the amount of time that passes from the moment of release to the moment when the projectile is at the top of its flight. Example: Start with: t = (v fy – v oy) / a y Plug in 0.0 m/s for v fy: t = (0.0 m/s – v oy) / a y Plug in values for v oy and a y: t = (0.0 m/s – 22.9 m/s) / – 9.8 m/s 2 t = -22.9 / -9.8 t = 2.33 t = 2.3 s In this example 3.3s of time passes while the projectile is rising to the top of the trajectory.